Explaining Differential Privacy in 3 Levels of Difficulty

When dealing with data anonymization, one inevitably encounters differential privacy. Many privacy researchers regard it as the “gold standard” of anonymization. Well-known tech companies such as Apple or Google are using it for certain data analyses and market it to raise public awareness underlining their focus on data protection. But what exactly stands behind this approach, and why does it have such a high reputation among privacy experts? Should now every company that analyze sensitive data use differential privacy?

In order to better understand the concept of differential privacy, we explain the technology in this article at three different difficulty levels and covering its advantages and disadvantages – in ascending difficulty. Hopefully, by the end of this article you will understand differential privacy at some level. So without further ado – let’s begin!

Difficulty Level: Easy

Explain It Like I’m 5

Your parents know a lot about you. Things like what vegetables you do not like. You might not want everybody to know this though. Being able to keep these types of secrets is called privacy. But the man who makes you lunch at daycare might want to know that there are children in the group that do not like tomatoes! He does not need to know if you are one of these children. It is enough if he can know that there are maybe 4 or 5 children who do not like tomatoes. This type of privacy is called differential privacy.

[Fast Forward 20 Years…]

Everyone should be aware of the importance of a full-fledged data and privacy protection in the digital age. Digital and data-driven business models are being developed in virtually every industry to deliver new products and services to customers. If everything runs smoothly, it is a classic win-win situation – the customer for example receives an unbeatable and tailor-made offer via newsletter for a trip to Japan, where he or she would like to go for ages, and the company boosts sales and saves expenses, as the marketing budget can be spent much more efficiently than before. This also means that you have to handle customers’ information with extreme care. Companies not always only know about preferences for travel destinations, but often also about much more private things, such as banks about transaction data or hospitals about patients’ illnesses.

Now suppose that a company wants to analyze its data, for instance to determine how well its targeting strategies are working. An anonymization mechanism based on differential privacy can help protect this sensitive data. Differential privacy itself is a mathematical definition of privacy. With this definition (in the form of the parameter epsilon, more on this later) it is possible to quantify exactly how secure or anonymous data is in a data set. “Anonymous” means that a person or group can no longer be identified. If an analyst works with such a data set, it is no longer possible for them to identify individual persons, but will only receive approximate statistics.

Having a mathematical proof of privacy was something entirely new in information science. Imagine it like inventing a car that’s 100% safe and can’t cause accidents. It is very much understandable that a lot of people are enthusiastic about such a concept!

Difficulty Level: Intermediate

Privacy Budget – Don’t You Spend It All At Once!

Of course math alone doesn’t anonymize a dataset by itself. There must be a mechanism and a proof that the mechanism reduces down to the math. Typically, differential privacy works by adding some noise to the data. Imagine it like pixelating a face to hide someone’s identity. The amount of noise added is a trade-off – adding more noise makes the data more anonymous, but it also makes the data less useful. In differential privacy, this trade-off is formally controlled using a parameter called epsilon (ε).

Different differential privacy mechanisms are used for different analytical tasks. There are now hundreds of published differentially private mechanisms, for instance for building a histogram, taking an average, releasing micro-data, or generating a machine learning model.

But first let’s get back to the trade-offs and the parameter epsilon: The problem is that when you use truly random noise to anonymize your data, every time you query the same data, you reduce the level of anonymization. This is because you are able to use the aggregate results to reconstruct the original data by filtering out the noise through averaging. The value epsilon is then used to determine how strict the privacy is. The smaller the value, the better the privacy but the worse the accuracy of any results from analysing the data. That also means, the smaller the value of epsilon, the fewer times you can access the data (effectively epsilon is proportional to your privacy budget) because otherwise you would be able to reconstruct the noise and ultimately de-anonymize the data. The trick to all this is that you can exactly define how much of your privacy budget you can use until the data is not considered as anonymous anymore.

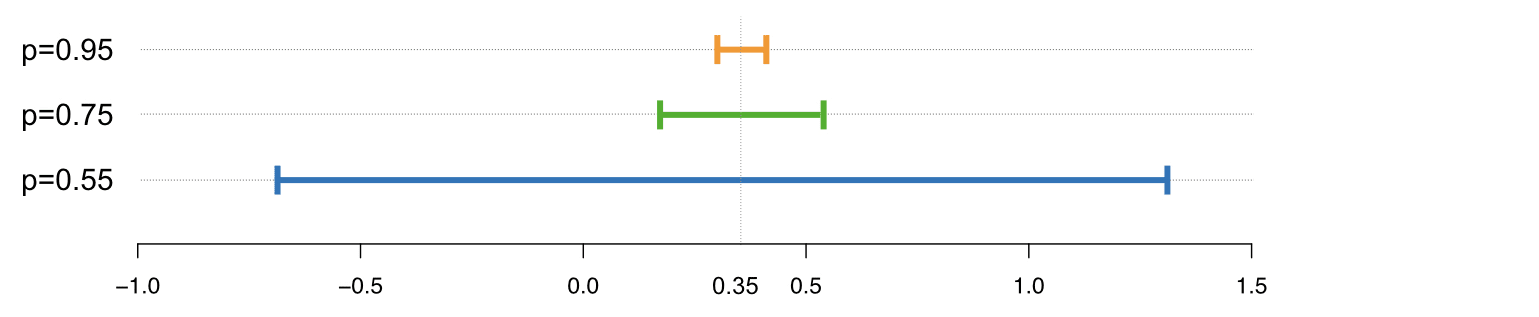
Picture Credit: Mark Hansen, https://accuracyandprivacy.substack.com/

As an example, in the picture above you can see how a low parameter has more privacy and the results range from -0.65 to 1.4. The higher the value of epsilon, the more accurate are the results but the privacy gets worse.

Difficulty Level: Professional

Uncertainty and Differential Privacy In Real-Life Applications

Now that we covered the basics, let’s have a closer look where uncertainty plays a major role in the concept. What we already learned is that the protection offered by a differentially private system comes from randomness — noise — that is added to data before publishing tables, or the results of other kinds of computations. The more noise, the greater the privacy protection.

The model itself expresses the abstract concept that if there are two databases that differ by only one user, the two databases are to a greater or lesser extent statistically indistinguishable from each other. The indistinguishability property holds even if an attacker knows everything about the data except whether this one user is included or not. The idea is that if an attacker can’t even tell if a user is in the data, he or she won’t be able to determine anything else about the user either.

The excellent blog article “Differential Privacy, an easy case” by journalism professor and IT-expert Mark Hansen explains this in a very comprehensible way.

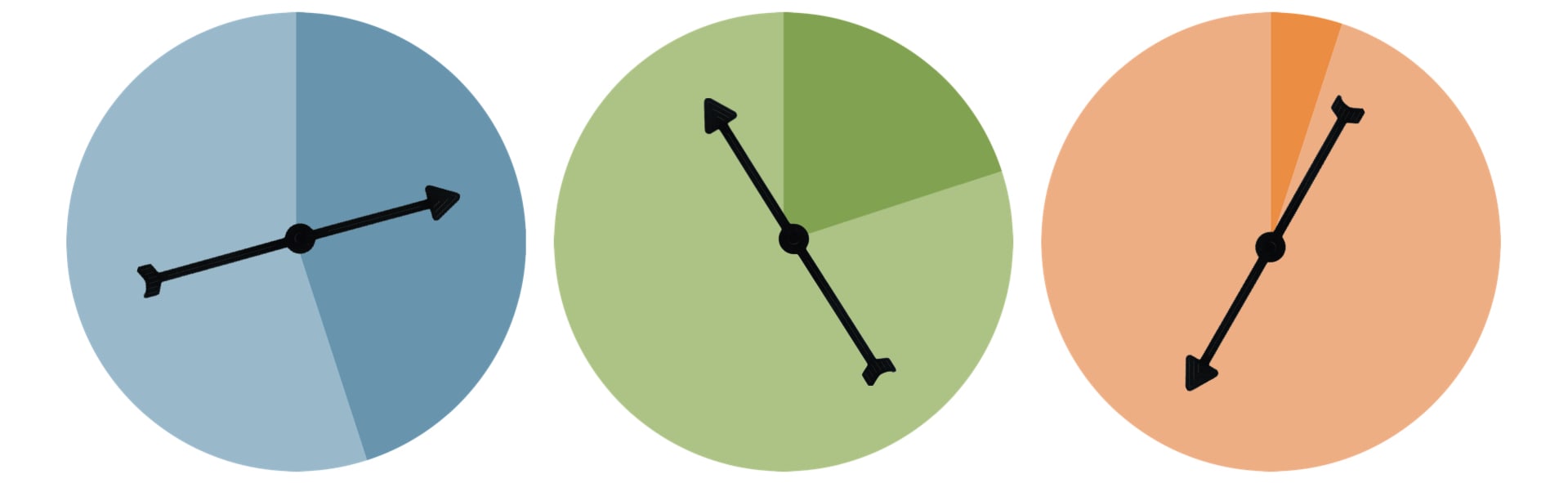
In his blog, Hansen compares and simplifies the privacy loss parameter with spinners that are tossed randomly and the result is either a “true” answer (light area) or “false” answer (dark area). The higher the epsilon, the smaller is the dark fraction in the dark area and the more likely it is to have a “true” answer by a survey participant.

It’s A Long Way To The Top

Enough for the theory – let’s have a deeper look at Differential Privacy in practice. In real life scenarios, the inventors of the concept suggested to keep the epsilon between 0.1 and 1. Unfortunately, deployments that honor composability and a value of ϵ that would generally be regarded as strongly anonymous (i.e. ϵ < 1) allow for only a small number of queries, maybe a few 10s. Some mechanisms, for instance Google and Apple’s, manage to avoid composability by making assumptions about the lack of correlation between attributes and for the same attribute over time. As a result, the number of queries they can make are unlimited, but the noise is high (errors in the 100s or 1000s for counts of users), and the ability to for instance observe correlations between attributes is lost. While these drawbacks are acceptable for the specific applications in Google and Apple, most analytic tasks require less noise and more query semantics.

As a result, many implementations of differential privacy have an epsilon of well over 10 and the privacy of the user in a dataset is not necessarily private. On the other hand, a mechanism with a small epsilon removes almost the entire information value. Moreover, the mathematical proof that a mechanism is actually Differential Privacy requires extensive expertise. Therefore, it is no coincidence that only companies with very high research expenditures use it with a published epsilon (cf. Differential Privacy Leaders You Must Know).

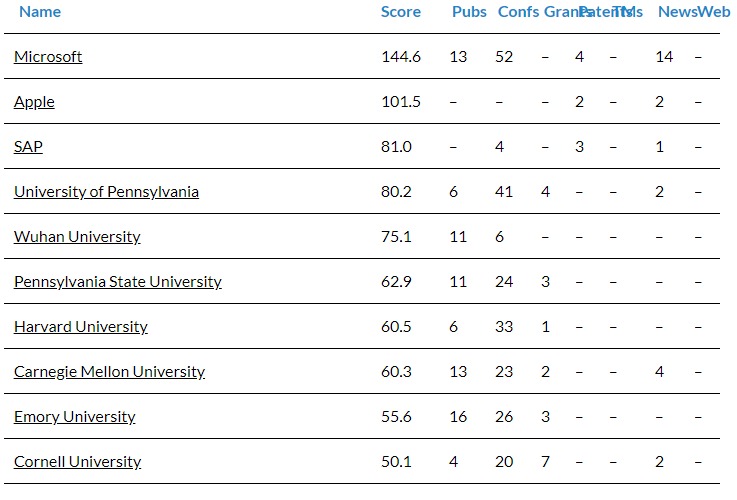
Top 10 entities worldwide leading innovations and advancements in Differential Privacy. Source: Linknovate.com

If you want to evaluate Differential Privacy for yourself there are some free anonymization tools which have a differential privacy integration that you can use to make your own experiments with. One of it is the Harvard Privacy Tools Project that has an implementation called PSI. Setting epsilon to 0.5, we could build user-count histograms of 3 columns and take the mean of two more. The tool estimated the 95% error on the mean to be 3%, and on the counts to be ±60 (around 5% to 10% for most of the histogram bars). These are reasonable and useful answers, but those 5 queries exhausted the budget. Were one to adhere strictly to differential privacy, that database (a small portion of the California Demographic Dataset) could never be queried again. A dataset with more rows could have allowed more queries at similar relative error levels, but regardless the budget prevents one from getting most of the analytic value from the dataset.

The ARX Data Anonymization Tool has a feature for generating differentially private microdata. Running this feature with an epsilon of 2 on a dataset with 16 columns and 5369 rows generates an anonymized dataset with no content whatsoever. Literally every value will be replaced by a ‘*’ symbol.

Another interesting use case is likely to happen in the near future at the US census bureau. They stated that they will use differential privacy for disclosure of 2020 census data. The public release of census data is a potential sweet spot for differential privacy, because the census bureau can carefully engineer how the privacy budget is used so as to maximize utility. A paper published by the Institute for Social Research and Data Innovation (ISRDI), however, argues that using differential privacy is overkill, and may severely compromise the utility of the census data. This is an important test case for differential privacy and it will be very interesting to see how it plays out.

Beautiful In Theory, Fallacy in Practice

Differential privacy is a beautiful theory. If it could be made to provide adequate utility while maintaining small epsilon, corresponding complete proofs, and reasonable assumptions, it would certainly be a privacy breakthrough. So far, however, this has rarely, and arguably never happened.

Last but not least, we can go back to the example of the 100% safe car. Imagine how such a car would look like? Probably more like a tank than a car: something not very suitable for everyday use.

(Non-Exhaustive) List Of Further Articles on Differential Privacy

Differential Privacy In The News
How One Of Apple’s Key Privacy Safeguards Falls Short

Beginner’s Articles on Differential Privacy
Differential Privacy: What Is It?
Differential Privacy, An easy case
Differential Privacy Leaders Must Know
Differential Privacy: A Primer for a Non-Technical Audience
Differential privacy in (a bit) more detail
Differential privacy in practice (easy version)
Almost differential privacy

On Choosing Epsilon
How Much Is Enough? Choosing ε for Differential Privacy
Differential Privacy: An Economic Method for Choosing Epsilon